| Distributed Coding of
Correlated Sources and Applications in Sensor Networks |
| Fusion storage and selective retreival of correlated sources |
Research Directions:
|
||||
|
Introduction
:
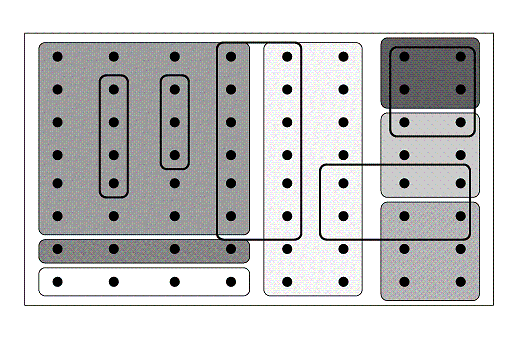 We are concerned with optimized storage of correlated streams of data, such that the time required for retrieving subsets of the streams, as defined by user requests, is minimized. This problem is directly motivated by the emergence of sensor networks, and the need to store their output for future retrieval and analysis. See Figure for a representative example. A new and challenging tradeoff between the amount of storage space and the average retrieval time in this case is due to the inter-source correlation. Specifically, if all streams are jointly compressed the storage cost will be minimized as the correlation between the streams can be fully exploited. However, this implies that all the stored data will need to be retrieved, even when only a small subset of the data streams is requested, which is extremely inefficient in terms of retrieval cost. On the other hand, if we store a separate description for every possible subset of streams (every possible query), the retrieval cost is certainly minimized, but the resulting storage cost will grow combinatorially.   |
||||
|
Lossless
Fusion Coding and Characterization of Achievable Rates :
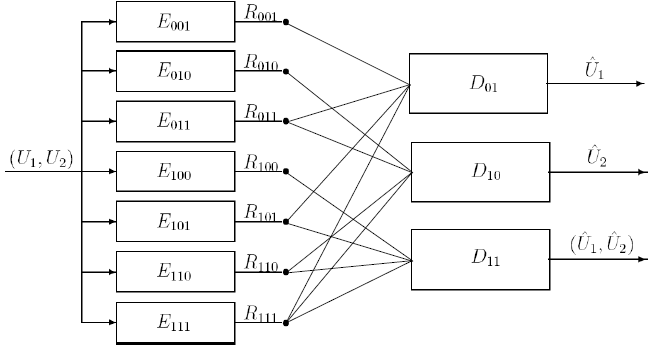 For memoryless sources, we investigated this tradeoff from an information theoretic perspective and obtained the corresponding performance bounds. We observed that it has direct connections with a known information-theoretic problem called multi-terminal source coding. By obtaining a characterization of the set of achievable rates for the source coding problem, we were able to completely characterize the storage versus retrieval tradeoff for the correlated streams storage problem. Since the rate region characterization that we obtained is asymptotic and not directly computable, we also developed a characterization of a (possibly strict) subset of the rate region that is computable at lower complexity. In order to do develop the achievable rate region, we break up the monolithic encoder output into bit-streams generated by component encoders. We maintain a separate decoder for each possible query and we partition the encoded bits into groups based on their access by the corresponding decoders. For 2 sources, we have 3 possible queries and hence 23-1=7 bit-streams. In general, for M sources, there are 2M-1 decoders 2(2M-1)-1 bit-streams. The bit-streams are termed "shared descriptions". Next, since all encoders have access to all sources, the achievable rate region remains the same if the encoders are assumed to be independent. Now, we can apply the Han and Kobayashi theorem for multi-terminal source coding and characterize the rates of the individual bit-streams. Available storage imposes constraints on the rate sum and over this region, the retrieval rate is minimized. Related publication: J. Nayak, S. Ramaswamy and K. Rose, "Correlated Source Coding for Fusion Storage and Selective Retrieval", IEEE International Symposium on Information Theory (ISIT) 2005.  |
||||
|
Fusion
Coder for Optimizing Storage Rate-Retrieval Rate-Distortion Tradeoff:
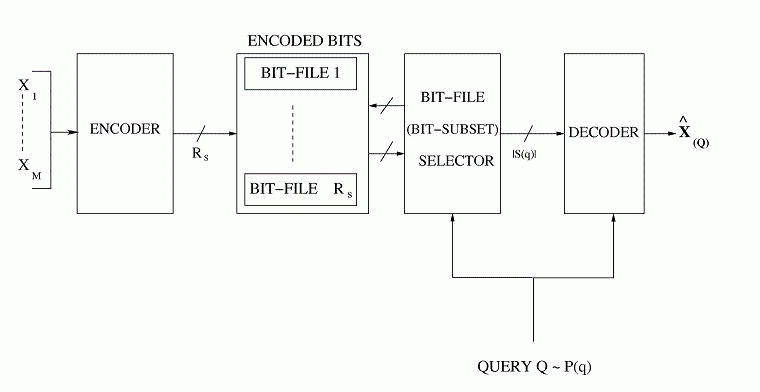 Based
on our earlier work on optimized storage and fast selective retrieval
of correlated streams of data, we developed information theoretical
models that estimate gains possible with selective information
retrieval over naive storage techniques. We then formulated a
Lagrangian cost function that is a weighted sum of the source and query
averaged distortion and the query-averaged retrieval rate, at a given
storage complexity. The optimization of this cost over a training set
of sample inputs and sample queries reduces to the design of an
encoding rule, a mapping from queries to subset of encoded bits and
code-books for different subsets of bits. We derived the necessary
conditions for optimality and minimized the cost function by
iteratively enforcing the necessary conditions for optimality. Since
each condition for optimality results in a reduced Lagrangian cost, the
algorithm is guaranteed to converge in a few iterations. We
investigated the performance of the algorithm over synthetic and real
data sets for query distributions representing expected user behavior
and compared the results with naive storage techniques - namely joint
compression, and separate compression.We evaluated the retrieval rate-distortion curves for our indexing for correlated data streams, and compared it with both 'naive' variants of joint and separate compression methods. Our method outperforms naive techniques at all retrieval speeds/distortions. Results on a set of 335 randomly generated queries over real and synthetic data-sets, indicate distortion gains of up to 3.5dB and retrieval speed-ups of up to 5X. Related publications: S. Ramaswamy, J Nayak and K. Rose,``Fusion coding of correlated sources for storage and selective retrieval,'' IEEE Transactions on Signal Processing, Vol. 58, Issue 4, pp 1722 - 1731, Mar 2010.  |
||||
|
Shared
Descriptions Fusion Coding:
 The design complexity of the proposed fusion coder grows
exponentially with the storage rate Rs.
Hence, the design of practical storage systems that handle hundreds of
streams, where it would be necessary to encode streams to a large
number of storage bits, would be unfeasible. Structural constraints on
the fusion coder would reduce the complexity. One such constrained
approach is the shared descriptions fusion coder. Here, queries are
mapped to one of several shared descriptions, each generated by a
low-complexity (low storage rate) encoder. By iteratively mapping
queries to descriptions and designing descriptions that are optimal for
the set of queries mapped to them, a constrained version of fusion
coder is designed. Note that the constraint is in the fact that while
encoders have access to all sources, the bit-selection for a query
would be restricted to the bits of the corresponding description. With
K shared descriptions, the complexity of design drops to O(K2Rs/K)
Preliminary experiments with 100 sensors, Rs=80 bits and K=16 descriptions, already show retrieval rate reductions by 7X and distortion reduction by 3-4dB. Note that the above general fusion coder design would be beyond computational reach, O(280) Related publications: S. Ramaswamy and K. Rose,``Shared descriptions fusion coding of correlated sources for storage and selective retrieval,'' manuscript under preparation. S. Ramaswamy and K. Rose, ``Shared descriptions fusion coding for storage and selective retrieval of correlated sources,'' Proc. IEEE Data Compression Conference (DCC), pp.262-271, March 2008. |
||||
|
Predictive Fusion Coding:
To compress sources with memory efficiently, we need to exploit temporal correlations, which are almost equally important to spatial correlations. Since fusion coding over long blocks is computationally intractable, we resort to a low complexity predictive fusion coder. However, design of optimal predictive fusion coders is complicated by the presence of a feedback loop and the need to handle an exponentially large query set at the encoder. 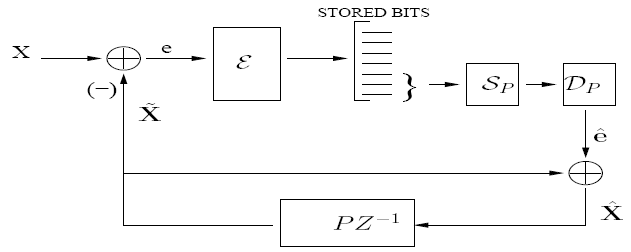 In our approach, we impose constraints on the number of encoder prediction loops that are allowed, where queries and sources share prediction loops. We present an extreme case (see figure above) with only one prediction loop. This leads to the need for a predictor bit-selector SP, in addition to the query bit-selector S(q), and due to the presence of the predictor bit-selector in the prediction loop, open loop design is not possible. Stable closed loop design is difficult due to the low rates considered and because if the loop is fully closed, we loose a "handle" on the error residuals. Hence, we resort to design by application of the "asymptotic closed loop" principle, which guarantees stability of design and optimality in performance (see figure below). 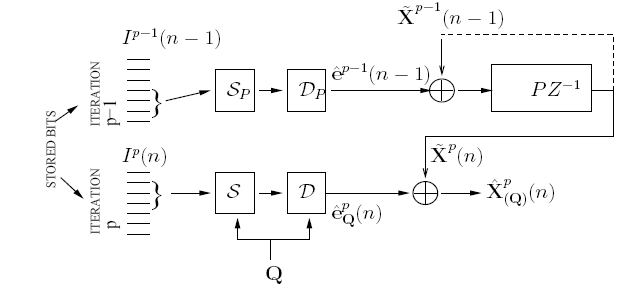 Related publications: S. Ramaswamy and K. Rose, ``Predictive fusion coding of correlated Sources,'' manuscript under preparation. |
SCL's Source coding and quantization archive
 |
|
 |