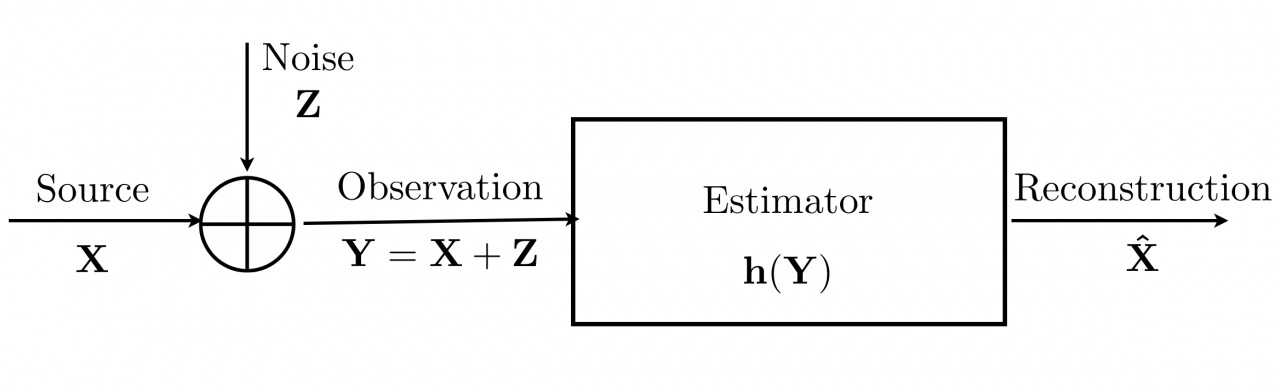
In this work, joint source channel coding with limited delay is considered. Most information theoretic results assume infinite amount of samples, which is not practically relevant, particularly for sensor networks where limited delay is an important key feature. In this work, optimal joint source-channel coding scheme for a given delay is studied. The point-to-point results are then extended to the main scheme of distributed source-channel coding of correlated sources. The obtained encoding functions are shown to be a continuous relative of, and in fact subsume as a special case, the Wyner-Ziv mappings encountered in digital distributed source coding systems, by mapping multiple source intervals to the same channel interval.

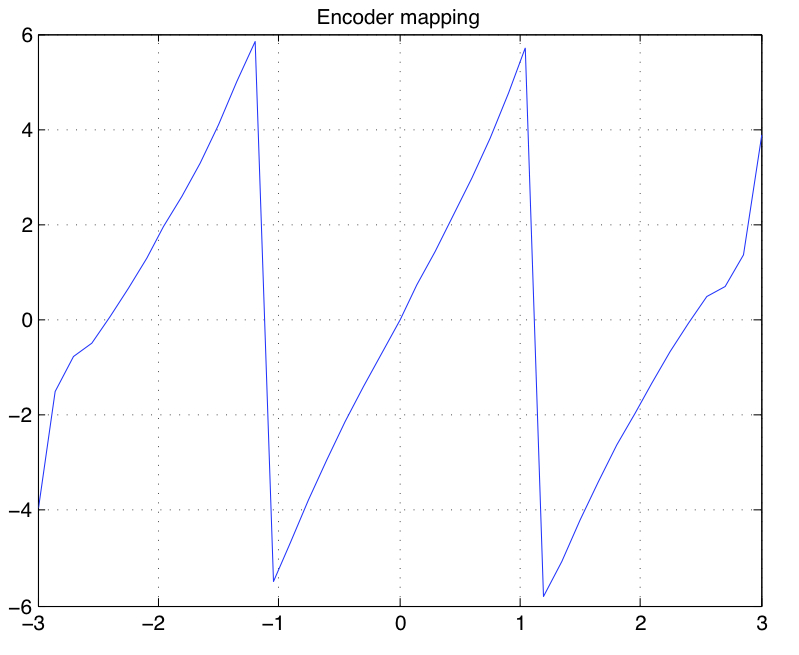
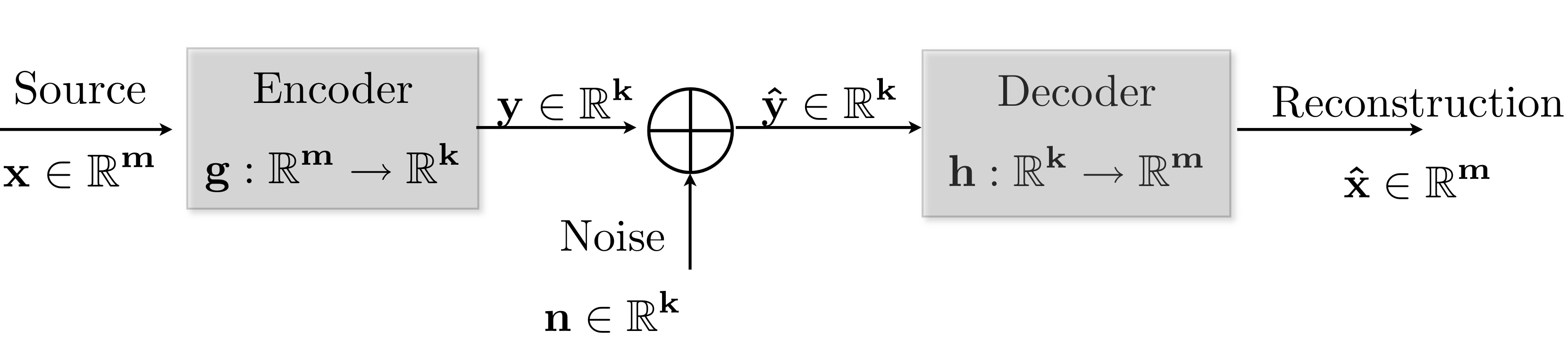
Method : The problem of obtaining the vector transformations (g and h in figure) that optimally map between the m-dimensional source space and the k-dimensional channel space is considered under a given channel power constraint and mean square error distortion measure. Closed form necessary conditions for optimality of the encoder and decoder mappings are derived. The optimal mappings are obtained using an iterative algorithm that updates encoder and decoder mappings according to optimality conditions at each iteration.

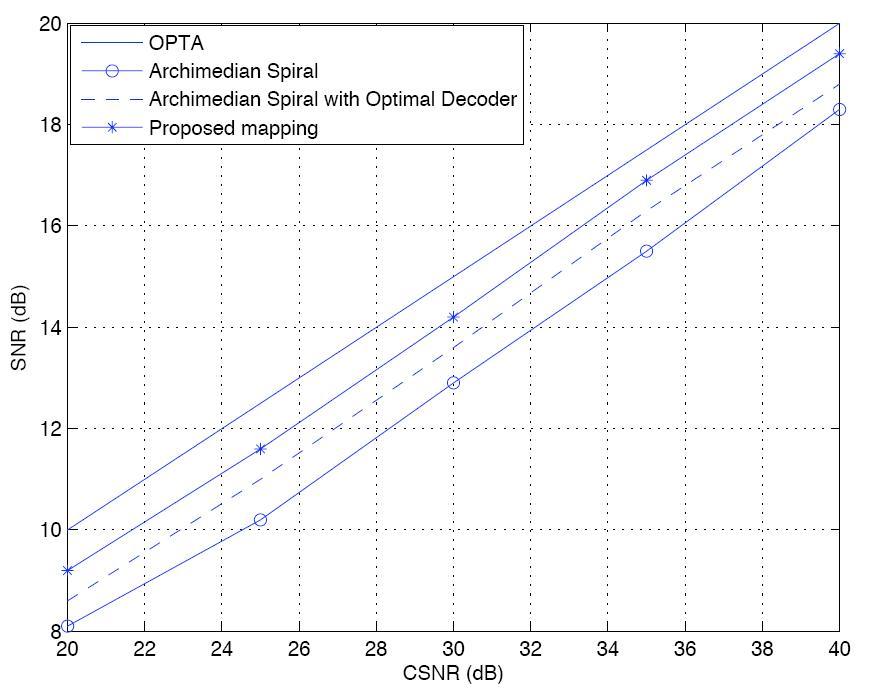
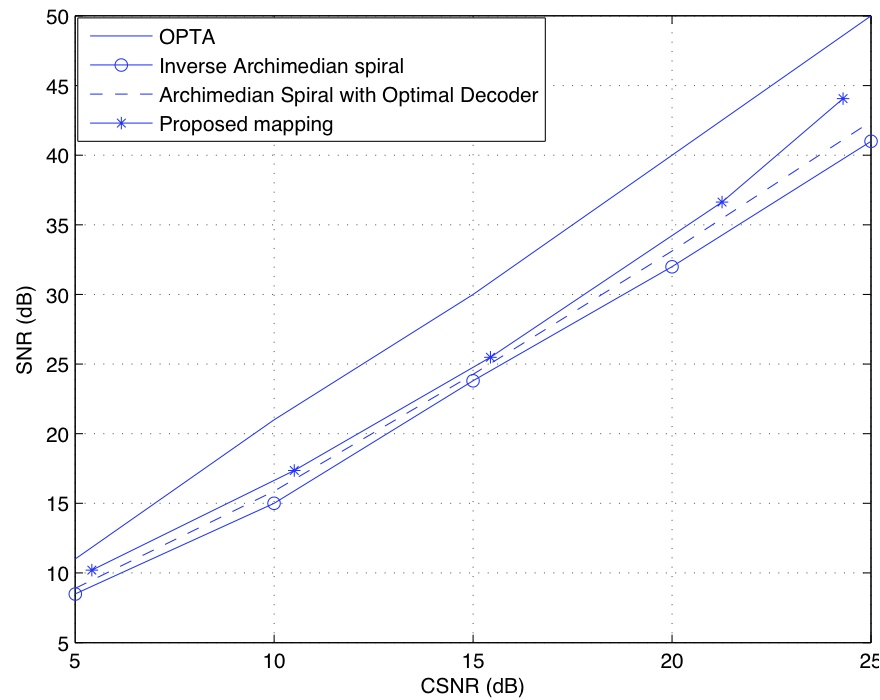
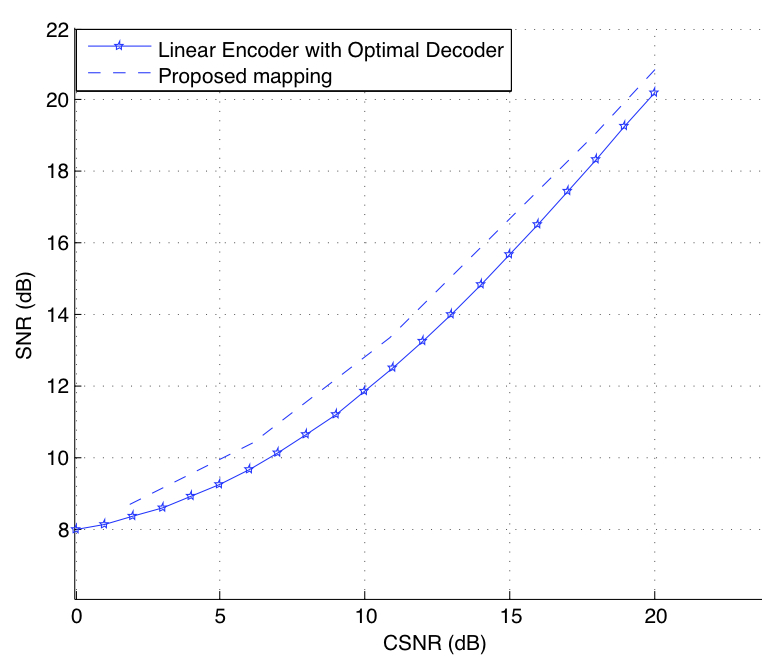
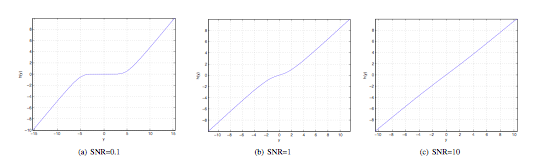
Results : Two representative results are presented. Although the proposed method is generally applicable, we present two representative examples based on Gaussian source and channel. The obtained mappings are compared to the prior works (that are based on Archimedian spiral) and as a benchmark, the theoretically optimal curve (OPTA) that can only be achieved with infinite delay. In the first one, two dimensional Gaussian source is mapped to scalar Gaussian channel, and in the second one, scalar Gaussian source is mapped to two dimensional vector channel. The results show substantial improvement of performance of proposed mappings over prior works.