Researchers: Sharadh Ramaswamy, Dr. Jayanth Nayak, Prof. Kenneth Rose
Introduction: We are concerned with optimized storage of correlated streams of data, such that the time required for retrieving subsets of the streams, as defined by user requests, is minimized. This problem is directly motivated by the emergence of sensor networks, and the need to store their output for future retrieval and analysis.
Fig 1: A 2D Sensor Field: Regions of Interest are Boxed and Shaded
See Figure 1 for a representative example. A new and challenging tradeoff between the amount of storage space and the average retrieval time in this case is due to the inter-source correlation. Specifically, if all streams are jointly compressed the storage cost will be minimized as the correlation between the streams can be fully exploited. However, this implies that all the stored data will need to be retrieved, even when only a small subset of the data streams is requested, which is extremely inefficient in terms of retrieval cost. On the other hand, if we store a separate description for every possible subset of streams (every possible query), the retrieval cost is certainly minimized, but the resulting storage cost will grow combinatorially.
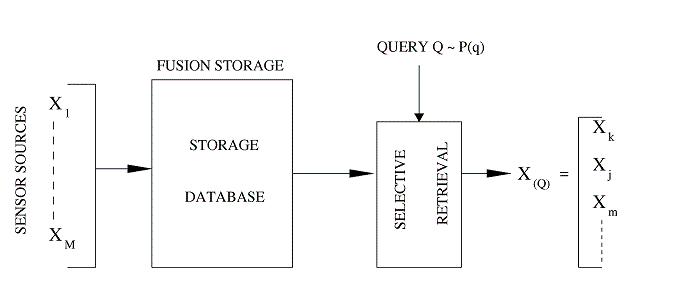
Fig 2: Fusion Storage vs. Selective Retrieval
Lossless Fusion Coding and Characterization of Achievable Rates:
For memoryless sources, we investigated this tradeoff from an information theoretic perspective and obtained the corresponding performance bounds (see publication no. 7). We observed that it has direct connections with a known information-theoretic problem called multi-terminal source coding. By obtaining a characterization of the set of achievable rates for the source coding problem, we were able to completely characterize the storage versus retrieval tradeoff for the correlated streams storage problem. Since the rate region characterization that we obtained is asymptotic and not directly computable, we also developed a characterization of a (possibly strict) subset of the rate region that is computable at lower complexity.
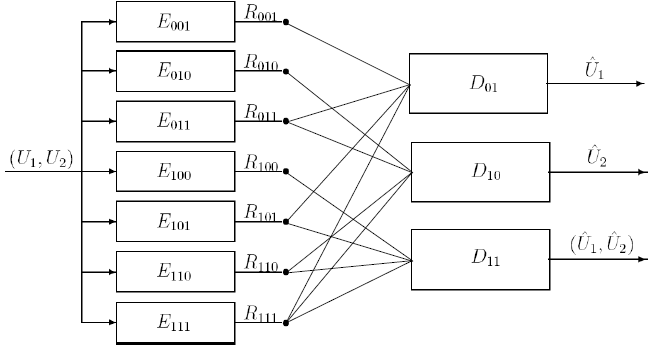
Fig 3: Encoder Decomposition for the 2 Source Case
In order to do develop the achievable rate region, we break up the monolithic encoder output into bit-streams generated by component encoders. We maintain a separate decoder for each possible query and we partition the encoded bits into groups based on their access by the corresponding decoders. For 2 sources, we have 3 possible queries and hence 23-1=7 bit-streams. In general, for M sources, there are 2M-1 decoders 2^(2M-1)-1 bit-streams. The bit-streams are termed "shared descriptions". Next, since all encoders have access to all sources, the achievable rate region remains the same if the encoders are assumed to be independent. Now, we can apply the Han and Kobayashi theorem for multi-terminal source coding and characterize the rates of the individual bit-streams. Available storage imposes constraints on the rate sum and over this region, the retrieval rate is minimized.
Fusion Coder for Optimizing Storage Rate-Retrieval Rate-Distortion Tradeoff:
Description: Based on our earlier work on optimized storage and fast selective retrieval of correlated streams of data, we developed information theoretical models that estimate gains possible with selective information retrieval over naive storage techniques. We then formulated a Lagrangian cost function that is a weighted sum of the source and query averaged distortion and the query-averaged retrieval rate, at a given storage complexity. The optimization of this cost over a training set of sample inputs and sample queries reduces to the design of an encoding rule, a mapping from queries to subset of encoded bits and code-books for different subsets of bits. We derived the necessary conditions for optimality and minimized the cost function by iteratively enforcing the necessary conditions for optimality. Since each condition for optimality results in a reduced Lagrangian cost, the algorithm is guaranteed to converge in a few iterations. We investigated the performance of the algorithm over synthetic and real data sets for query distributions representing expected user behavior and compared the results with naive storage techniques - namely joint compression, and separate compression.
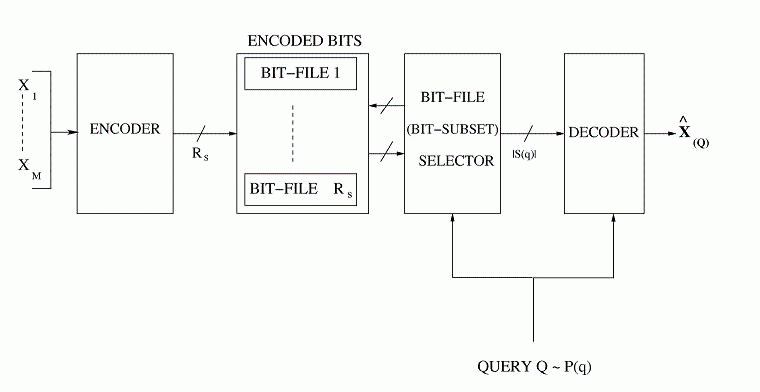
Fig 4: Proposed Fusion Coder Operation
Results: We evaluated the retrieval rate-distortion curves for our indexing for correlated data streams, and compared it with both 'naive' variants of joint and separate compression methods. Our method outperforms naive techniques at all retrieval speeds/distortions. Preliminary results on a set of 335 randomly generated queries over real and synthetic data-sets, indicate distortion gains of up to 3.5dB and retrieval speed-ups of up to 5X (see publication no. 13).
Shared Descriptions Fusion Coding:
Description: The design complexity of the proposed fusion coder grows exponentially with the storage rate Rs. Hence, the design of practical storage systems that handle hundreds of streams, where it would be necessary to encode streams to a large number of storage bits, would be unfeasible. Structural constraints on the fusion coder would reduce the complexity. One such constrained approach is the shared descriptions fusion coder. Here, queries are mapped to one of several shared descriptions, each generated by a low-complexity (low storage rate) encoder. By iteratively mapping queries to descriptions and designing descriptions that are optimal for the set of queries mapped to them, a constrained version of fusion coder is designed. Note that the constraint is in the fact that while encoders have access to all sources, the bit-selection for a query would be restricted to the bits of the corresponding description. With K shared descriptions, the complexity of design drops to O(K2Rs/K)
Shared Descriptions Fusion Coder
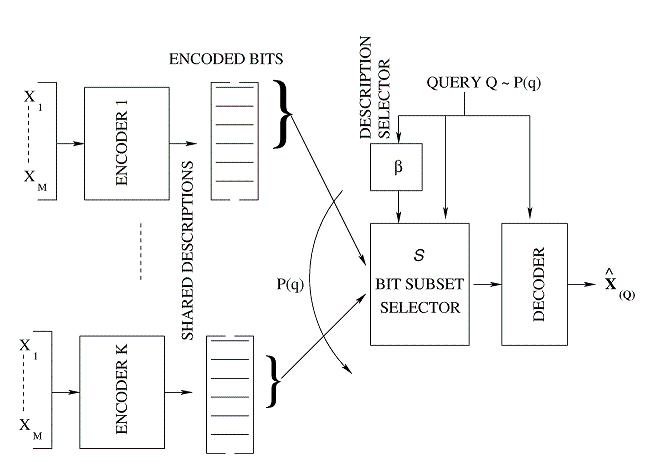
Fig 5: Proposed Shared Descriptions Fusion Coder
Results: Preliminary experiments with 100 sensors, Rs=80 bits and K=16 descriptions, already show retrieval rate reductions by 7X and distortion reduction by 3-4dB. Note that the above general fusion coder design would be beyond computational reach, O(280) (see publication no. 19).
Predictive Fusion Coding:
To compress sources with memory efficiently, we need to exploit temporal correlations, which are almost equally important to spatial correlations. Since fusion coding over long blocks is computationally intractable, we resort to a low complexity predictive fusion coder. However, design of optimal predictive fusion coders is complicated by the presence of a feedback loop and the need to handle an exponentially large query set at the encoder.
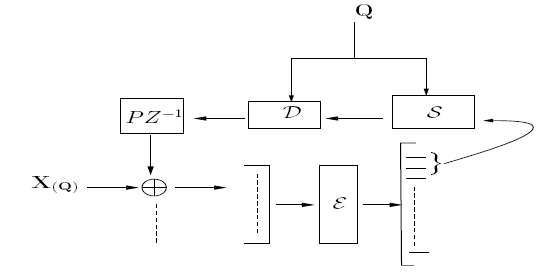
Fig. 6: Optimal Predictive Fusion Coding
In our approach, we impose constraints on the number of encoder prediction loops that are allowed, where queries and sources share prediction loops. We present an extreme case (see Figure 7) with only one prediction loop. This leads to the need for a predictor bit-selector SP, in addition to the query bit-selector S(q), and due to the presence of the predictor bit-selector in the prediction loop, open loop design is not possible. Stable closed loop design is difficult due to the low rates considered and because if the loop is fully closed, we loose a "handle" on the error residuals. Hence, we resort to design by application of the "asymptotic closed loop" principle, which guarantees stability of design and optimality in performance (see Figure 8).
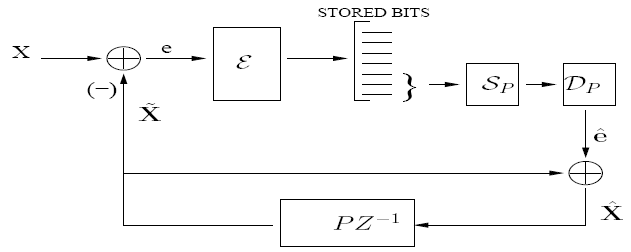
Fig. 7: Constrained Predictive Fusion Coding: Encoder (1 Prediction Loop allowed)
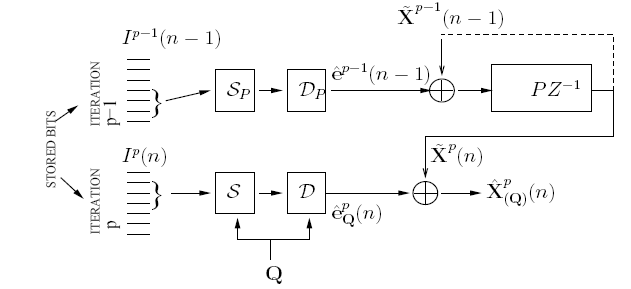
Fig. 8: Constrained Predictive Fusion Coding Design By Asymptotic Closed Loop: Decoder (1 Prediction Loop allowed)